3月の学習ポイント・ 中学2年生

中学2年生の3月の数学の学習は確率、データの分布となります。
確率は学調テスト、高校入試問題など全ての実力テストで出題される単元です。
しかも点が取りやすい単元でもあります。
言いかえれば理解しやすい単元でありテストの出題率が高い単元となります。
数学が苦手な生徒でも確率では点が取れると思う生徒が多いようです。
確率の求め方は大きく分けると樹形図を書いて求めるものと表をかいて求めるものの2つのパターンに分けられます。
⑴ 樹形図により求める確率
樹形図をかいて起こりえる全部の場合の数が何通りあるのか求める。
そのうちことがらの起こる場合の数が何通りかを求めて確率を求める。
\[確率=\frac{ことがらの起こる場合の数}{起こりえる全部の場合の数}\]
樹形図をかく場合に
選んで順番を決める場合なのか。
ただ同時に選ぶだけで順番は関係ない場合なのか。
この違いで場合の数が変わります。
ただ同時に選ぶだけで順番は関係ない場合が分からないという生徒が多くいます。
同時に選ぶだけで順番は関係ないときの樹形図は重複している組合せはかかないようにします。
(A, B)と(B, A)は重複しているので(A, B)だけで考えます。
樹形図も(A, B)だけで(B, A)はかきません。
これが分かりにくい要因です。
ただ、確率を求める場合ならばどちらも同じ確率になります。
確率に関してはこだわる必要はありません。
たとえば、A、B、C、D の4枚のカードからA、Bの2枚のカードを選ぶ確率を求めます。
本来であればただ同時に選ぶだけで順番は関係ないので樹形図は重複をしている組合せはかかないで場合の数を求めます。
かいた樹形図よりA、Bが含まれる場合の数を求め確率を出します。
重複をしている組合せをかかない樹形図で確率を求める。
(通常の確率の求め方)
全部の場合の数=6通り
A、Bが含まれる場合の数=1通り
\[確率=\frac{ことがらの起こる場合の数}{起こりえる全部の場合の数}\]
\[確率=\frac{1}{6}\]
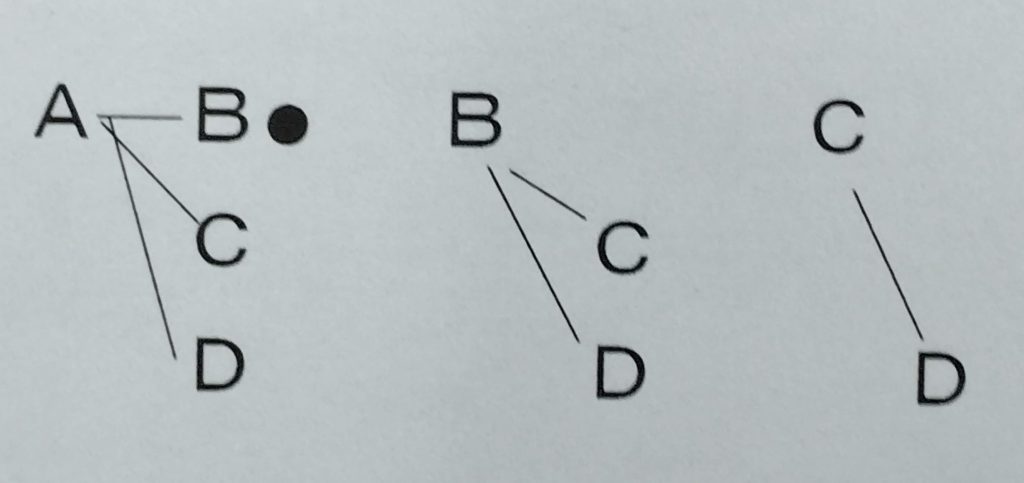
重複をしている組合せをかいた樹形図で確率を求める。
(起こる場合全部の数は違っている)
全部の場合の数=12通り
A、Bが含まれる場合の数=2通り
\[確率=\frac{2}{12}\]
\[ =\frac{1}{6}\]

どちらも確率は同じになります。
場合の数は変わりますが確率を求めるだけの問題では確率は同じ答えになるので気にしなくてもよいことになります。
⑵ 表により求める確率
2つのサイコロの確率問題は表を作って考える。
大小2つのさいころを同時に投げるとき、出る目の数の和が7になる確率を求める。
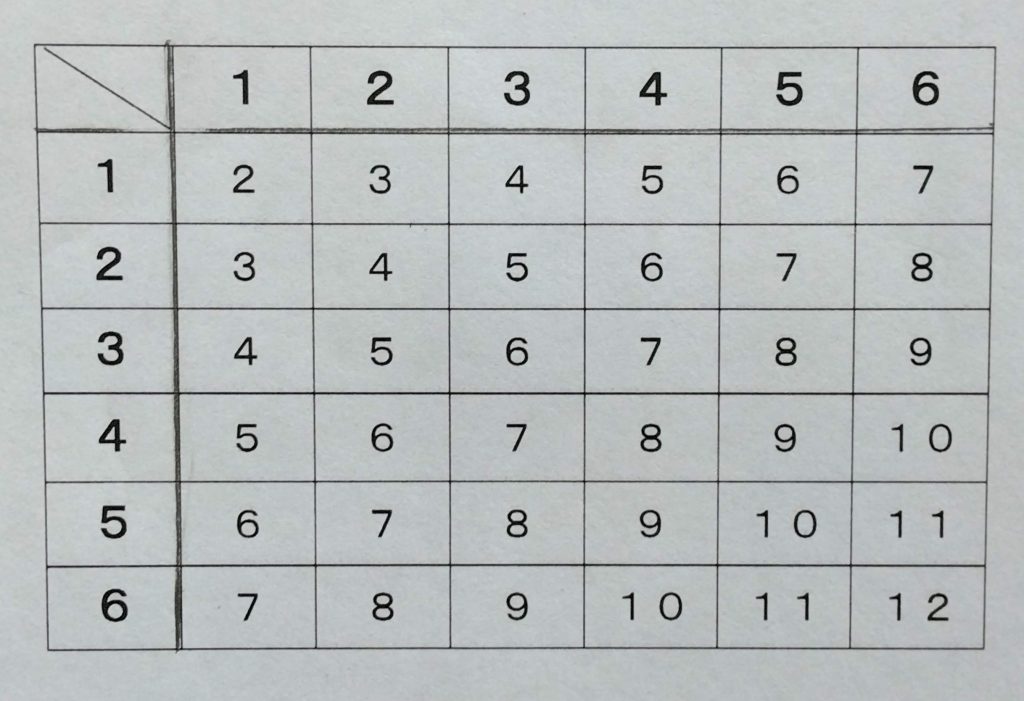
2つのサイコロ問題の全ての場合の数は6×6=36通りになる。
表より目の数の和が7になるのは6通りある。
\[確率=\frac{6}{36}\]
\[ =\frac{1}{6}\]
確率は高校入試まで実力テストでは必ず出題される単元であり、また点が取れる単元であることを意識して学習することが大切です。


