3月の学習ポイント・ 中学1年生

中学1年生の3月の数学の学習は空間図形・データの活用となります。
空間図形の注意点
直線と平面・2平面の位置関係において
⑴ 辺と垂直な面を求める。
辺ABと垂直な面を求める時に辺ABを辺とする面も答えとしてしまう。
下の図において
辺ABと垂直な面はどれか。
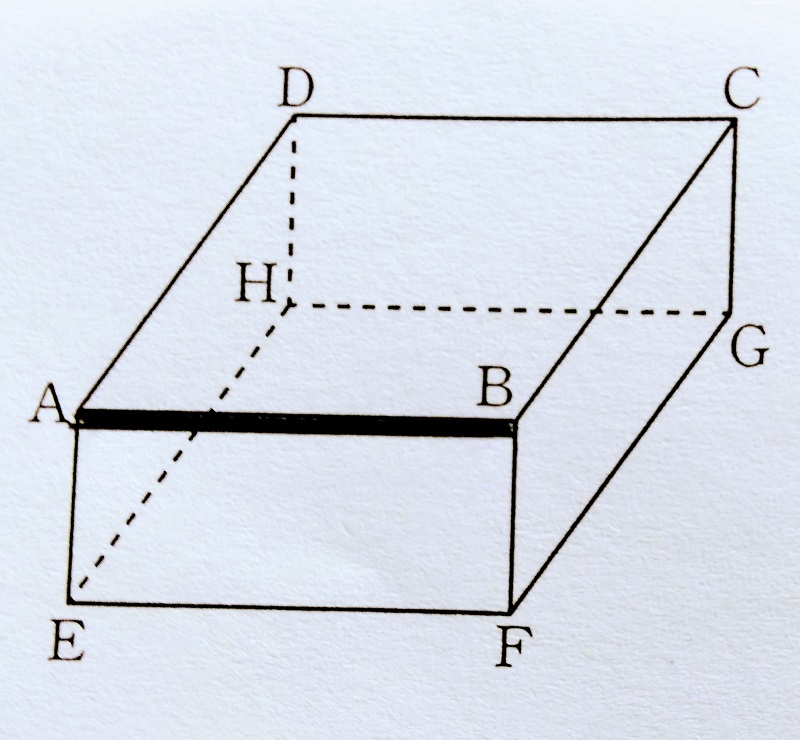
答に面ABCD、面AEFBを答えとすると間違いになります。
面ABCD、面AEFBともに辺ABを含む面となり辺ABと垂直な面とはなりません。
これが間違いやすいので注意してください。
答は面AEHD、面BFGCとなります。
⑵ ねじれの位置にある辺を求める。
ねじれの位置にある辺を求める時のポイント。
ねじれの位置ではない辺をピックアップして残った辺をねじれの位置とする。
ねじれの位置ではない辺とは
① 辺ABと接している辺(点A、点Bを起点とする辺)
② 辺ABと平行な辺
以上2つに該当する辺を探して色付けする。
色付けされていない残った辺がねじれの位置にある辺となる。
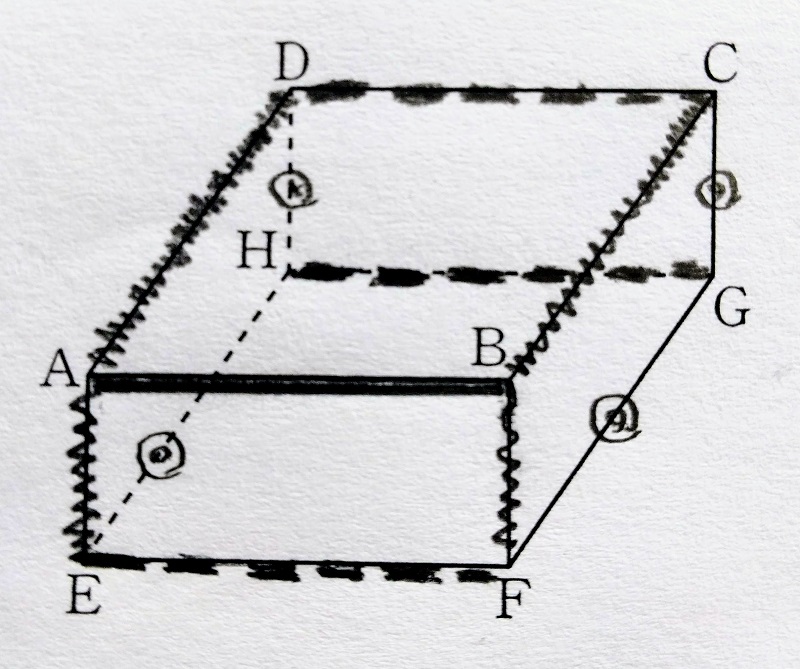
下図において
辺ABとねじれの位置にある辺を求めよ。

ねじれではない辺を色づけする。
① 辺ABと接している辺
辺AD、AE、BC、BF
② 辺ABと平行である辺
辺EF、HG、DC
上記①②以外の残った辺がねじれの位置にある辺になる。
答 辺CG、FG、DH、EH
表面積・体積問題
⑶ 円すいの表面積の求め方を覚えておく。
円すいの表面積・中心角を求める問題は学調テストなど実力テストでの出題率が高いのでできるようにしておく。
側面積(おうぎ形)・中心角を簡単に求める公式があるのでそれを使って求めるようにする。
教科書通りの求め方をすると多くの生徒がむずかしいと感じる問題であるが簡単な公式を覚えるだけで問題を解くことができる。
円すいの表面積は側面積+底面積で求められる。
底面積は円の面積。
下図において
円すいの側面積を求めよ。
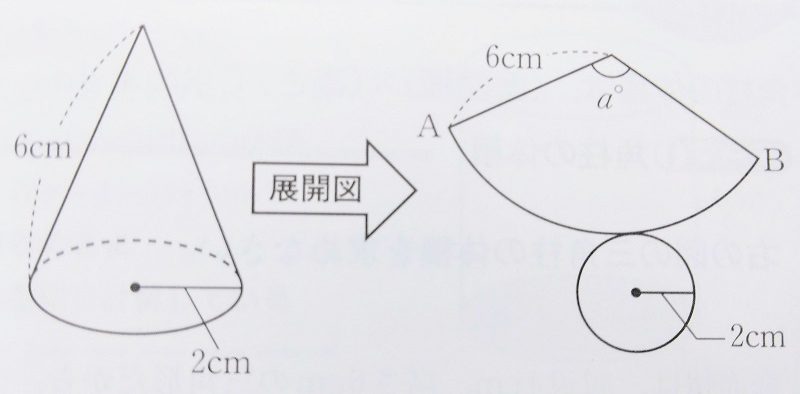
教科書通りに円すいの側面積を求めてみる。
側面積(おうぎ形)の弧の長さは底面の円の周の長さと同じなので
2×2×π=4π
おうぎ形の中心角をa°とすると
おうぎ形のもとの円の周の長さは
6×2×π=12π
おうぎ形の中心角a°は
a=360°×\(\frac{4π}{12π}\)
=360°×\(\frac{1}{3}\)=120°
a=120°
おうぎ形の面積=円の面積×\(\frac{中心角}{360°}\)より
6×6×π×\(\frac{120}{360}\)
=36π×\(\frac{1}{3}\)=12π
答は 12π\(cm^{2}\)
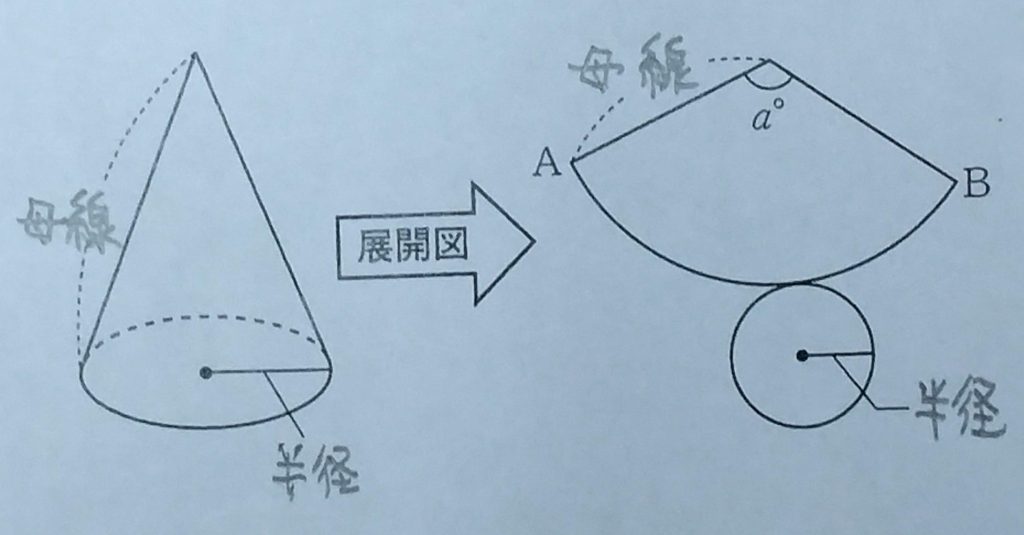
公式を使って求める。
公式
① 側面積(おうぎ形)=π×母線×半径
② 中心角=360°×\(\frac{半径}{母線}\)
上記の問題では
母線=6 半径=2 より
側面積(おうぎ形)=π×6×2=12π
よって 答は 12π\(cm^{2}\)
こんなに簡単に求めることができる。


