5月の学習ポイント②・中学３年生

中学３年生の５月の数学の学習は「因数分解」「因数分解の利用」となります。

因数分解②

いろいろな因数分解

(1) 共通因数をくくり出して因数分解

共通因数でくくり残りの式を因数分解する。

① \(ax^{２}+6ax+9a\)
共通因数\(a\)でくくる。
＝\(a\)(\(x^{2}+6x+9\))
=\(a\)\((x+3)^{2}\)

② \(5ax^{２}+25ax+20a\)
共通因数\(5a\)でくくる。
＝\(5a\)(\(x^{2}+5x+4\))
=\(5a\)\((x+1)(x+4)\)

(2) 式を文字におきかえる因数分解

共通な式をM,Aなどにおきかえて因数分解しおきかえた文字をもとにもどす。

①\((x+y)^{2}+4(x+y)+3\)
共通な式\(x+y\) をMにおきかえる。
\(x+y\) ＝Mとおくと
＝\(M^{2}+4M+3\)
公式を使って因数分解する。
=\((M+1)(M+3)\)
おきかえた文字Mをもとの式にもどす。
＝\((x+y+1)(x+y+3)\)

② \((x+2)^{2}-(y+3)^{2}\)
\(x+2\)＝A、\(y+3\)＝Ｂ とおくと
＝\(A^{2}-Ｂ^{2}\)
公式を使って因数分解する。
=\((A+B)(A-B)\)
おきかえた文字をもとの式にもどす。
(　)を書いてもどす。
＝{\((x+2)+(y+3)\)}{\((x+2)-(y+3)\)}
かっこをはずす。
かっこの前のマイナスの符号に注意する。
＝\((x+2+y+3)\)\((x+2-y-3)\)
同類項をまとめる。
＝\((x+y+5)\)\((x-y-1)\)

よくある間違い
＝{\((x+2)+(y+3)\)}{\((x+2)-(y+3)\)}
かっこをはずす。
かっこの前がマイナスの符号のときは符号が変わる。
＝\((x+2+y+3)\)\((x+2-y+3)\)
かっこをはずしたときに符号が変わっていない間違い。

(3) 同類項をまとめる因数分解

\(x\)をふくむ項とふくまない項に分けて考える。

①\(ax+x+a+1\)
\(x\)をふくむ項とふくまない項に分ける。
\(ax+x+a+1\)
＝\((ax+x)+(a+1)\)
\(x\)をふくむ項を\(x\)でくくる。
=\(x(a+1)+(a+1)\)
\(a+1=M\) とおくと
=\(xM+M\)
\(M\) でくくる。
=\(M(x+1)\)
\(M\) をもとの式にもどす。
=\((a+1)(x+1)\)

式の利用

(1) 数の性質

数の表し方は整数\(n\) を使って
連続する２つの整数 … \(n, n+1\)…
連続する２つの偶数 … \(2n, 2n+2\)…
連続する２つの奇数 … \(2n+1, 2n+3\)…
と表す。

\(n\) の倍数であることの証明は
式が「\(n\)×整数」の形で表せることを示せばよい。

① 連続する２つの偶数の２乗の和は４の倍数になることを証明する。

(証明)
連続する２つの偶数は整数\(n\) を使って
\(2n, 2n+2\) と表される。
この２数の２乗の和は
　(\(2n)^{2}\)＋(\(2n+2)^{2}\)
＝\(4n^{2}+4n^{2}+8n+4\)
＝\(8n^{2}+8n+4\)
＝\(4(2n^{2}+2n+1)\)
\(n\) は整数なので \((2n^{2}+2n+1)\) は整数となる。
よって\(4(2n^{2}+2n+1)\) は４の倍数となる。
したがって
連続する２つの偶数の２乗の和は４の倍数になる。

数の性質の証明では証明のパターンがあるのでそのパターンを覚えるようにする。

数の性質の証明パターン
…した数は５の倍数になることを証明する場合
条件を整数\(n\) を使って式に表す。
５の倍数を証明する場合は ５×整数の形にするので
式を５( ) の形になるように変形する。
５( ) の形に変形できたならば以下のように書く。
( ) は整数なので５( ) は５の倍数となる。
したがって…は５の倍数となる。

８の倍数であることを証明する場合は
８( ) の形になるように変形して
( ) は整数なので８( ) は８の倍数となる。
したがって…は８の倍数となる。

上記の赤い部分が証明のパターンになる。
証明する倍数の数値を変えて書く。

(2) 数の計算のくふう

乗法公式や因数分解を利用して数の計算を簡単にする。

① \(65^{2}-15^{2}\)
\(x^{2}－a^{2}＝(x+a)(x－a)\) を使う。
\(65^{2}-15^{2}\)
＝(６５＋１５)(６５－１５)
＝８０×５０
＝４０００

② \(51^{2}\)
\((x+a)^{2}\)＝\(x^{2}+2ax+a^{2}\) を使う。
\(51^{2}\)
＝\((50+1)^{2}\)
＝\(50^{2}+2×50×1+1^{2}\)
＝２５００＋１００＋１
＝２６０１

③ ５２×４８
\((x+a)(x－a)\)＝\(x^{2}－a^{2}\)を使う。
５２×４８
＝(５０＋２)(５０－２)
＝\(50^{2}-2^{2}\)
＝２５００－４
＝２４９６

(3) 図形の性質の証明

証明のパターンを覚える
\(S=al\) の証明
\(S=a(　　)\)　 …①
\(l=(　　)\)　 …②
\(a×②\)
\(al＝a\)(　　)　 …③
①③より
\(S=al\)

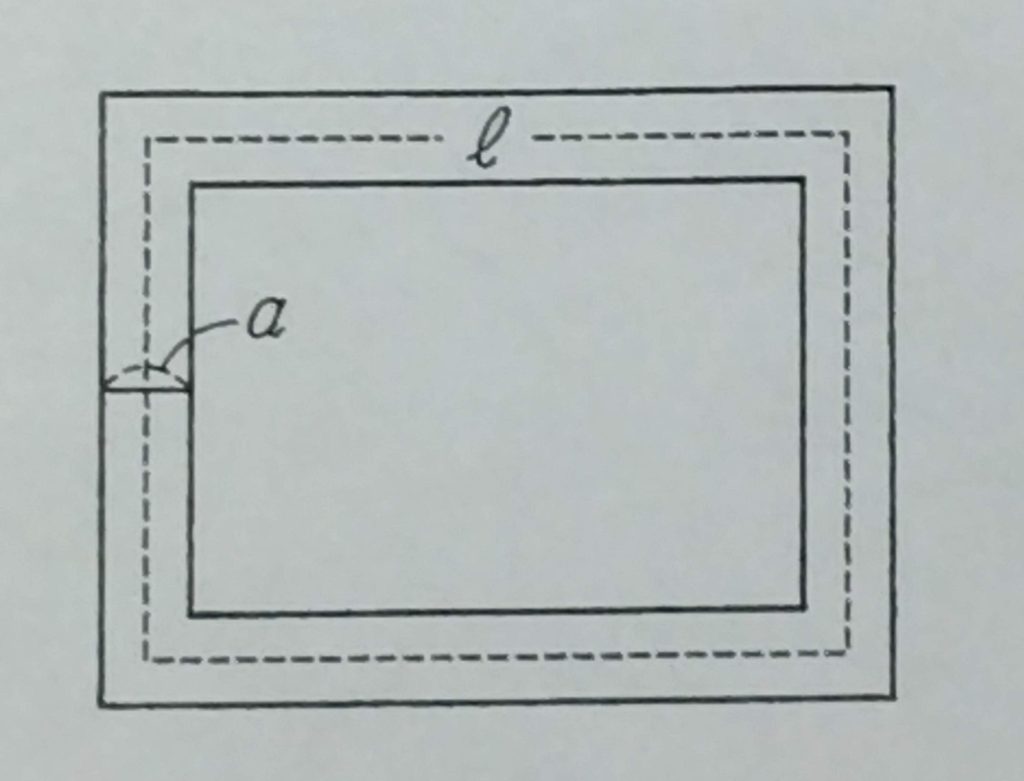
① 下図のように長方形の土地の周囲に幅\(a\) の道がある。
この道の面積を \(S\) 、道の中央を通る線の長さを \(l\) とするとき、
\(S=al\) となる。
このことを長方形のたての長さを\(b\) 、横の長さを\(c\) として証明しなさい。

(証明)
\(S=(b+2a)(c+2a)-bc\)
\( =bc+2ab+2ac+4a^{2}-bc\)
\( =4a^{2}+2ab+2ac\)　 …①
\(l=2(b+a)+2(c+a)\)
　\(　=2b+2a+2c+2a\)
　\(　=4a+2b+2c\)　 …②
\(a×②\)より
\(al＝a(4a+2b+2c)\)
　\(＝4a^{2}+2ab+2ac\)　 …③
①③より
\(S=al\)

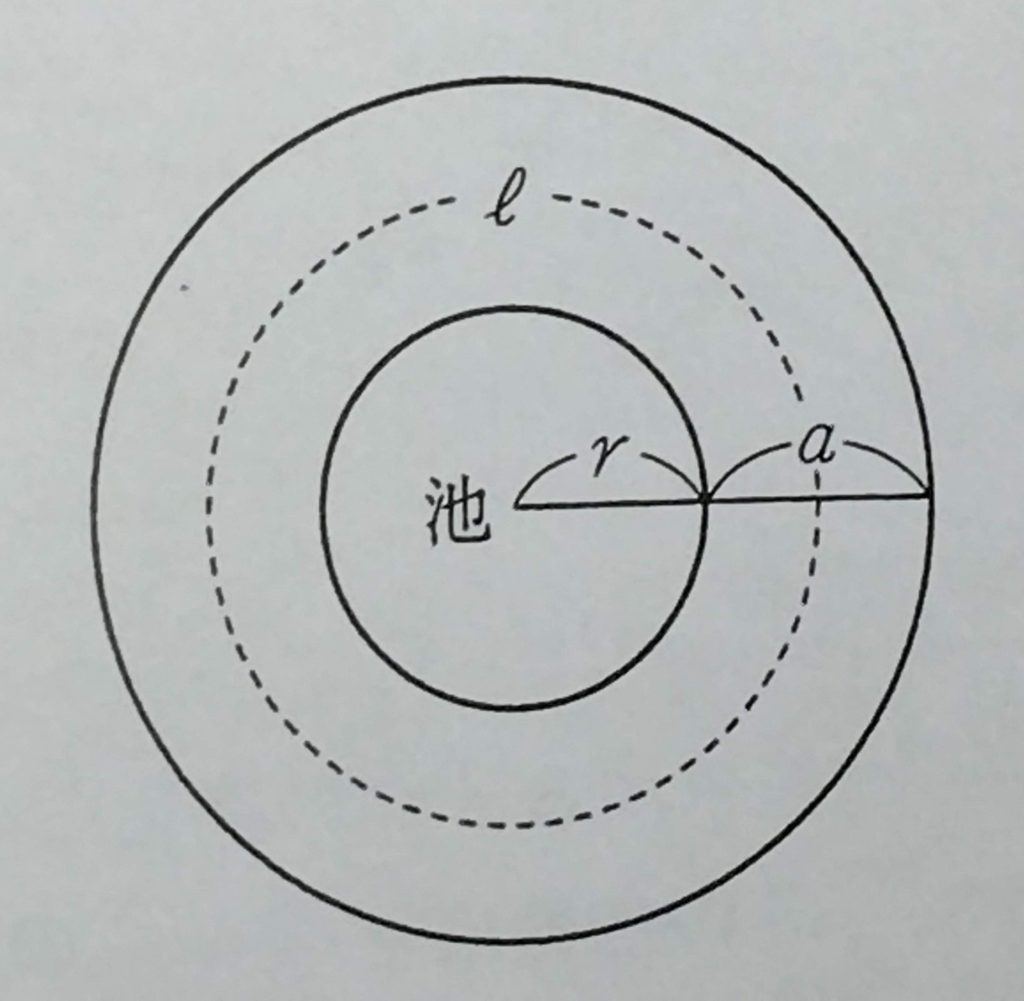
② 下図のような半径 \(r\) の円形の池の周りに幅\(a\) の道がある。
この道の面積を \(S\) 、この道の中央を通る円周の長さを \(l\) とするとき、
\(S=al\) であることを証明しなさい。

(証明)
\(S=π(r+a)^{2}-πｒ^{2}\)
\( =π(r^{2}+2ar+a^{2})-πｒ^{2}\)
\( =πr^{2}+2πar+πa^{2}-πｒ^{2}\)
\( =2πar+πa^{2}\) 　 …①
\(l=2(r+\)\(\frac{a}{2}\)\()π\)
　\(　=2π(r+\)\(\frac{a}{2}\)\()\)
　\(　=2πr+πa\)　 …②
\(a×②\)より
\(al＝a(2πr+πa)\)
　\(＝2πar+πa^{2}\)　 …③
①③より
\(S=al\)